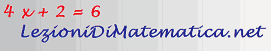LEGGE DEI RENDIMENTI MARGINALI DECRESCENTI
COME SI PRESENTA LA FUNZIONE DI PRODUZIONE SECONDO LA LEGGE DEI RENDIMENTI MARGINALI DECRESCENTI
FUNZIONE DI PRODUZIONE CON UN SOLO FATTORE VARIABILE
Si è visto, nelle lezioni precedenti, che la funzione di produzione con un solo fattore variabile può avere vari andamenti. Può essere:
Spesso, però, quello che accade è che la funzione di produzione non ha sempre lo stesso andamento, cioè non è sempre costante, crescente o decrescente all'aumentare del fattore lavoro, e ciò è dovuto alla così detta legge dei rendimenti marginali decrescenti.
LEGGE DEI RENDIMENTI MARGINALI DECRESCENTI
La legge dei rendimenti marginali decrescenti afferma che, quando aumentiamo l'impiego di un fattore produttivo, lasciando invariate le quantità impiegate degli altri fattori, il prodotto marginale diventa via via minore. La quantità totale prodotta continua ad aumentare, fino ad un certo punto. Successivamente, aumentando ulteriormente l'impiego del fattore variabile la quantità totale prodotta inizia a diminuire.
Tutto questo si verifica perché le prime unità di input impiegate hanno una produttività marginale crescente, mentre via via che la quantità di tale input aumenta, la produttività marginale diventa decrescente.
Esempio. Supponiamo che un imprenditore disponga di un appezzamento di terreno che rappresenta il fattore produttivo costante.
Egli assume un lavoratore da far lavorare su tale terreno. L'impiego del lavoratore permette di ottenere un dato
output. Chiaramante la quantità prodotta
sarà uguale al prodotto marginale del lavoratore.
Supponiamo che l’imprenditore decida di assumere un secondo lavoratore: la quantità complessivamente prodotta aumenterà e tale aumento è uguale alla produttività marginale
del secondo lavoratore, che non coincide necessariamente con quella del primo lavoratore. Potrebbe accadere che la seconda unità di lavoro tragga beneficio dall’aiuto
della prima, riuscendo ad aumentare la quantità prodotta più di quanto avesse fatto il primo lavoratore da solo. In questo caso il
prodotto marginale cresce.
Ad un certo punto, continuando ad aumentare la forza lavoro, la quantità di prodotto aggiuntiva dovuta all'impiego di ogni nuovo lavoratore comincierà a ridursi
pur continuando ad aumentare (per lo meno inizialmente) la produzione totale. Le cause della riduzione della produttività marginale possono essere varie: ad esempio
può accadere che quando il numero dei lavoratori diventa elevato, essendo l'appezzamento di terreno limitato, l'aggiunta di nuova manodopera risulti
controproducente perché gli operai finiscono con l'intralciarsi tra loro creando problemi organizzativi.
Se il numero di lavoratori continua a crescere ulteriormente, si arriverà, ad un certo punto, ad avere addirittura una riduzione della quantità totale prodotta.
La legge dei rendimenti marginali decrescenti è valida, in genere, nel breve periodo perché nel lungo periodo la quantità impiegata di tutti i fattori è variabile.
Tornando all'esempio precedente, nel lungo periodo l'imprenditore può acquistare un ulteriore appezzamento di terreno in modo che, aumentando il numero dei lavoratori impiegati, essi non si intralcino tra loro.
Tuttavia, anche nel lungo periodo, potrebbe accadere che l'impresa non voglia variare alcuni fattori produttivi che, quindi, restando costanti, potrebbero rendere valida la legge dei rendimenti marginali decrescenti.
ESEMPIO
Riportiamo, di seguito, un esempio.
| Ore di lavoro (L) | Quantità prodotta (Q) | Prodotto medio (Q/L) | Aumento di Q (ΔQ) | Aumento di L (ΔL) | Prodotto marginale (ΔQ/ΔL) |
|---|---|---|---|---|---|
| 1 | 5 | 5,00 | 5 | 1 | 5 |
| 2 | 12 | 6,00 | 7 | 1 | 7 |
| 3 | 22 | 7,33 | 10 | 1 | 10 |
| 4 | 34 | 8,50 | 12 | 1 | 12 |
| 5 | 42 | 8,40 | 8 | 1 | 8 |
| 6 | 48 | 8,00 | 6 | 1 | 6 |
| 7 | 53 | 7,57 | 5 | 1 | 5 |
| 8 | 55 | 6,88 | 2 | 1 | 2 |
| 9 | 54 | 6,00 | -1 | 1 | -1 |
| 10 | 51 | 5,10 | -3 | 1 | -3 |
GRAFICO DELLA FUNZIONE DI PRODUZIONE
Qui sotto abbiamo il grafico della funzione di produzione relativo all'esempio precedente.
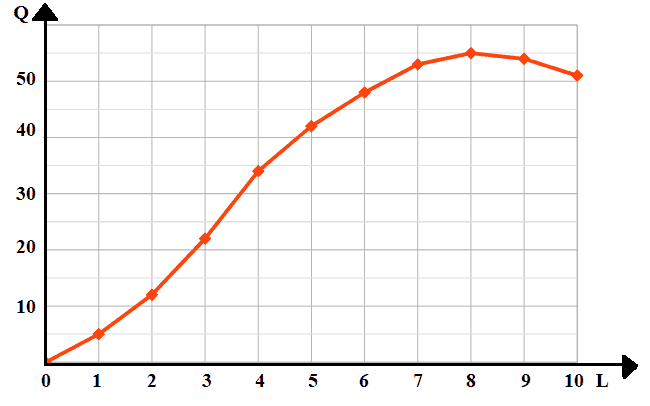
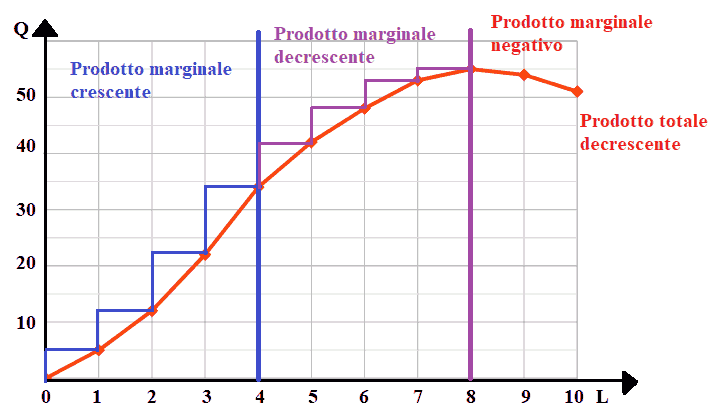
La funzione ha tre andamenti diversi:
- nella prima parte, fino a quando il lavoro raggiunge le 4 unità, il prodotto marginale del lavoro è
crescente: ad ogni aumento del fattore lavoro corrisponde un aumento della quantità prodotta via via maggiore (graficamente, ogni scalino disegnato
in blu è più alto rispetto a quello precendente).
Il prodotto totale cresce al crescere del fattore lavoro.
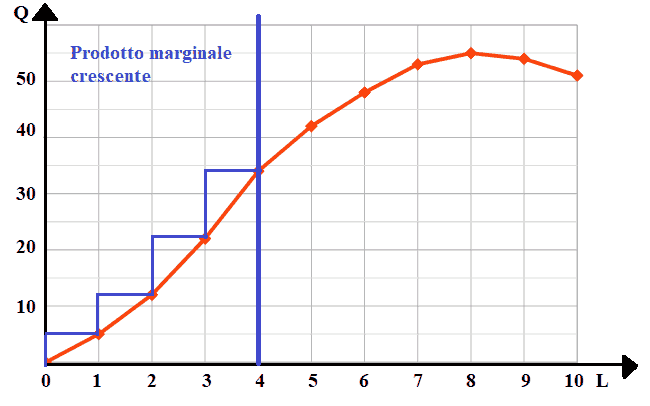
- nella seconda parte, quando il lavoro supera le 4 unità e fino alle 8 unità, il prodotto marginale del lavoro è
decrescente: ad ogni aumento del fattore lavoro corrisponde un aumento della quantità prodotta via via inferiore
(graficamente, ogni scalino disegnato in viola è più basso rispetto a quello precendente.
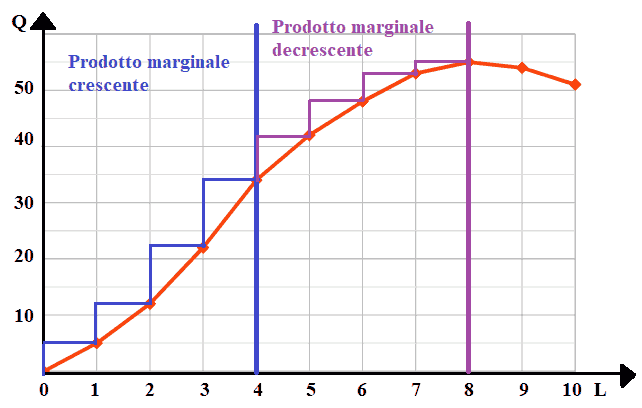
Anche in questa area il prodotto totale cresce al crescere del fattore lavoro.
- nella terza parte, quando il lavoro supera le 8 unità il prodotto marginale del lavoro diventa
negativo: il prodotto totale inizia a diminuire
nonostante il fattore lavoro impiegato stia continuando a crescere.