FUNZIONE DI PRODUZIONE CON UN SOLO FATTORE VARIABILE

FUNZIONE DI PRODUZIONE CON UN SOLO FATTORE

Supponiamo che la quantità prodotta di un dato bene (quantità che indicheremo con Q) dipenda da due fattori produttivi: il fattore lavoro (L) e il fattore capitale (K). La funzione di produzione, quindi, è data da:

Q = f (L, K)

Inoltre ipotizziamo che il capitale sia fisso, in altre parole l'impresa non può variare la quantità di capitale impiegato. Invece, la quantità di lavoro impiegata è variabile.

In questo caso la quantità prodotta dall'impresa dipende esclusivamente dalla quantità di lavoro impiegata: la nostra funzione di produzione è una funzione ad un solo fattore ed esattamente:

Q = f (L)

Per poter variare la quantità prodotta l'impresa deve variare la quantità di lavoratori impiegati nel processo produttivo.

PRODOTTO TOTALE

Quando la funzione di produzione dipende da un solo input viene chiamata anche funzione del prodotto totale.

Spesso, tale funzione, anziché essere indicata nel modo appena visto, cioè:

Q = f (L)

viene indicata nel modo seguente:

Q = f (L, K)

dove il simbolo

K

si legge

K sovrasegnato

e sta ad indicare che il fattore K ha un valore costante.

GRAFICO DELLA FUNZIONE DEL PRODOTTO TOTALE

Poiché la quantità prodotta varia al variare del solo input utiilizzato, la funzione può essere rappresentata sugli assi cartesiani riportando:

• sull'asse delle ascisse il fattore produttivo variabile (nell'esempio precedente il lavoro);
• sull'asse delle ordinate la quantità di prodotto.

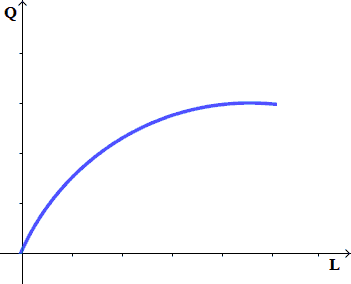
L'aspetto del grafico della funzione totale non è sempre lo stesso come avremo modo di dire parlando di funzioni di produzione lineari e funzioni di produzione non lineari.

Un modo in cui la funzione si può presentare è il seguente:

PRODOTTO MEDIO

Per prodotto medio si intende la quantità prodotta mediamente da ogni lavoratore.

Il prodotto medio si ottiene dividendo la quantità totale prodotta per il numero di lavoratori impiegati.

In simboli possiamo scrivere:

AP_L = Q/L

dove:

AP_L è il prodotto medio del lavoro

Q rappresenta la quantità totale prodotta

L rappresenta la quantità di fattore lavoro impiegata.

Esempio: se l'impresa ottiene, nell'arco di un mese, 30 unità di prodotto impiegando 5 operai il prodotto medio è 6. Ciò indica che ogni operaio produce mediamente 6 unità di prodotto al mese.

PRODOTTO MARGINALE O PRODUTTIVITA' MARGINALE

Per prodotto marginale del lavoro o produttività marginale del lavoro si intende la quantità aggiuntiva prodotta in seguito all'aumento di una unità del fattore lavoro.

Possiamo indicare la produttivià marginale del lavoro, in simboli nel modo seguente:

MP_L = ΔQ/ ΔL

che si legge

Produttività marginale del lavoro uguale a delta Q fratto delta L

dove:

MP_L è la produttività marginale del lavoro

ΔQ rappresenta l'incremento della quantità prodotta

ΔL rappresenta l'incremento del fattore lavoro

Esempio: supponiamo che la nostra impresa assuma un ulteriore operaio in modo da averne 6 anziché 5. Ipotizziamo, inoltre, che in seguito all'aumento del fattore lavoro, la quantità prodotta nel corso di un mese passi da 30 a 36. L'incremento della quantità prodotta, pari a 6, costituisce il prodotto marginale del lavoro.

Nel nostro esempio, prodotto medio e prodotto marginale coincidono, ma non è sempre così come avremo modo di capire meglio parlando di prodotto marginale crescente, costante e decrescente.

SIMBOLI

Il prodotto medio viene indicato con simbolo AP che deriva dai termini inglesi Average Product, ma può essere indicato anche col simbolo PMa.

Il prodotto marginale è generalmente indicato con il simbolo MP che deriva dall'espressione inglese Marginal Product.

Tuttavia esso viene a volte indicato anche con altri simboli come PMg oppure PMa.