FUNZIONE DI PRODUZIONE LINEARE
LA PENDENZA DELLA FUNZIONE DI PRODUZIONE LINEARE
FUNZIONE DELLA PRODUZIONE: UN ESEMPIO
Nella tabella che segue riportiamo un esempio di funzione della produzione con un solo fattore variabile (il fattore lavoro L).
La tabella indica il fattore lavoro impiegato, la quantità prodotta in corrispondenza di ogni livello del lavoro, il calcolo del prodotto medio (Q/L) e del prodotto marginale (ΔQ/ΔL).
| Ore di lavoro (L) | Quantità prodotta (Q) | Prodotto medio (Q/L) | Aumento di Q (ΔQ) | Aumento di L (ΔL) | Prodotto marginale (ΔQ/ΔL) |
|---|---|---|---|---|---|
| 1 | 5 | 5 | 5 | 1 | 5 |
| 2 | 10 | 5 | 5 | 1 | 5 |
| 3 | 15 | 5 | 5 | 1 | 5 |
| 4 | 20 | 5 | 5 | 1 | 5 |
| 5 | 25 | 5 | 5 | 1 | 5 |
FUNZIONE DI PRODUZIONE LINEARE
Come si può notare dalla tabella, l'incremento del fattore lavoro porta un incremento proporzionale della quantità prodotta. In altre parole il prodotto marginale del fattore lavoro è costante.
Notiamo, inoltre, che il prodotto medio e il prodotto marginale sono sempre uguali.
E' chiaro che se la produttività marginale è costante, ogni volta che aumenta di una unità il fattore lavoro, il prodotto marginale rimane invariato come pure il prodotto medio.
La funzione da noi riportata è una funzione di produzione lineare.
Tale funzione è del tipo:
Q = a·L
Nel nostro caso
a = 5
e la funzione diventa:
Q = 5·L
GRAFICO DELLA FUNZIONE DI PRODUZIONE LINEARE
Andiamo a disegnare la nostra funzione sugli assi cartesiani riportando sull'asse delle ascisse il fattore lavoro e su quello delle ordinate la quantità prodotta:
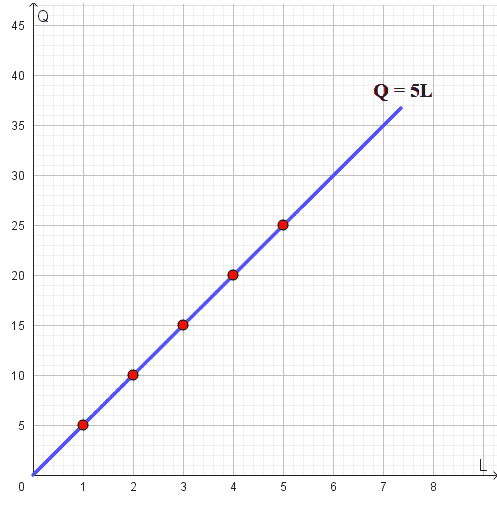
Quindi, possiamo dire che, quando la produttività marginale del lavoro è costante la funzione della produzione è una retta che parte dell'origine degli assi.
PENDENZA DELLA FUNZIONE DI PRODUZIONE LINEARE
Ora supponiamo che vi sia un progresso tecnologico in seguito al quale, impiegando la stessa quantità del fattore lavoro, si riesce ad ottenere una maggiore quantità di prodotto.
Ad esempio, la situazione potrebbe diventare la seguente:
| Ore di lavoro (L) | Quantità prodotta (Q) | Prodotto medio (Q/L) | Aumento di Q (ΔQ) | Aumento di L (ΔL) | Prodotto marginale (ΔQ/ΔL) |
|---|---|---|---|---|---|
| 1 | 10 | 10 | 10 | 1 | 10 |
| 2 | 20 | 10 | 10 | 1 | 10 |
| 3 | 30 | 10 | 10 | 1 | 10 |
| 4 | 40 | 10 | 10 | 1 | 10 |
| 5 | 50 | 10 | 10 | 1 | 10 |
Disegniamo, la nuova funzione di produzione, accanto a quella precedente:
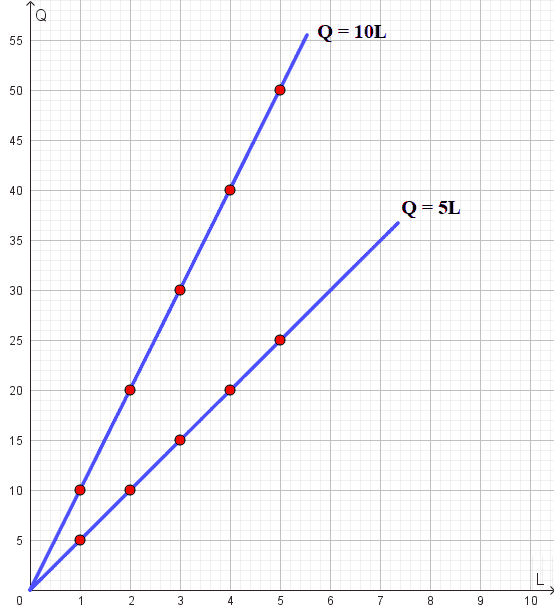
Notiamo che anche la nuova funzione è una funzione lineare dato che il prodotto marginale è costante. Tuttavia la nuova funzione ha una pendenza maggiore rispetto alla pendenza della precedente funzione: è chiaro che questo è dovuto al fatto che, a parità di lavoro impiegato, la quantità prodotta è maggiore. Per essere più precisi possiamo dire che all'aumentare del fattore lavoro di una unità, la quantità prodotta cresce in misura maggiore rispetto all'esempio precendente (aumenta di 10 unità anziché di 5 unità).
Poiché il rapporto tra la variazione della quantità prodotta e la variazione di una unità del fattore lavoro rappresenta il prodotto marginale è evidente che, quando il prodotto marginale è maggiore la pendenza della curva è maggiore e viceversa.
PENDENZA DELLA FUNZIONE DI PRODUZIONE E PRODOTTO MARGINALE
Ricapitolando possiamo dire che, la pendenza della funzione di produzione, quando il prodotto marginale è costante (e quindi la funzione è rappresentata da una retta), è uguale al prodotto marginale stesso: maggiore è il prodotto marginale del lavoro e maggiore è la quantità prodotta a parità di ore di lavoro.
La maggiore pendenza della funzione di produzione, a parità di altre condizioni, è dovuta ad un impiego del fattore lavoro migliore grazie all'uso di una tecnologia più vantaggiosa.