FUNZIONE DI PRODUZIONE NON LINEARE
FUNZIONE DI PRODUZIONE CON RENDIMENTI CRESCENTI E FUNZIONE DI PRODUZIONE CON RENDIMENTI DECRESCENTI
FUNZIONE DELLA PRODUZIONE NON LINEARE
Abbiamo visto che una funzione di produzione con un solo fattore variabile, quando il prodotto marginale di tale fattore è costante, è una funzione di produzione lineare.
Ora vediamo, invece, cosa accade quando il prodotto marginale è crescente oppure decrescente. Ovviamente, in tali ipotesi, non ci troviamo di fronte ad una funzione di produzione lineare.
FUNZIONE DELLA PRODUZIONE A RENDIMENTI CRESCENTI
Riportiamo, nella tabella che segue, un esempio di come varia la produzione al variare del fattore lavoro. La tabella include anche il calcolo del prodotto medio (Q/L) e del prodotto marginale (ΔQ/ΔL).
| Ore di lavoro (L) | Quantità prodotta (Q) | Prodotto medio (Q/L) | Aumento di Q (ΔQ) | Aumento di L (ΔL) | Prodotto marginale (ΔQ/ΔL) |
|---|---|---|---|---|---|
| 1 | 5 | 5 | 5 | 1 | 5 |
| 2 | 11 | 5,5 | 6 | 1 | 6 |
| 3 | 18 | 6 | 7 | 1 | 7 |
| 4 | 26 | 6,5 | 8 | 1 | 8 |
| 5 | 35 | 7 | 9 | 1 | 9 |
Come si può notare, nell'esempio riportato all'aumentare del fattore lavoro la quantità prodotta aumenta. L'aumento del prodotto avviene in misura via via crescente: quindi ci troviamo di fronte ad una funzione di produzione a rendimenti crescenti in quanto il prodotto marginale del lavoro è crescente.
In questa ipotesi, all'aumentare del fattore lavoro aumenta il prodotto marginale e, di conseguenza, aumenta anche il prodotto medio. L'aumento del prodotto medio è comunque inferiore rispetto all'aumento del prodotto marginale.
GRAFICO DELLA FUNZIONE DI PRODUZIONE A RENDIMENTI CRESCENTI
Graficamente, la funzione riportata nell'esempio precedente, si presenta così:
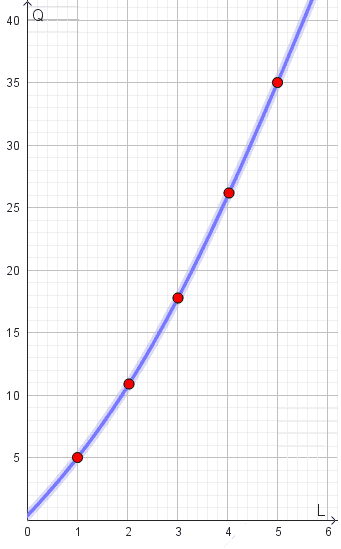
Come possiamo notare la funzione è convessa.
FUNZIONE DELLA PRODUZIONE A RENDIMENTI DECRESCENTI
Vediamo un altro esempio.
| Ore di lavoro (L) | Quantità prodotta (Q) | Prodotto medio (Q/L) | Aumento di Q (ΔQ) | Aumento di L (ΔL) | Prodotto marginale (ΔQ/ΔL) |
|---|---|---|---|---|---|
| 1 | 9 | 9 | 9 | 1 | 9 |
| 2 | 17 | 8,5 | 8 | 1 | 8 |
| 3 | 24 | 8 | 7 | 1 | 7 |
| 4 | 30 | 7,5 | 6 | 1 | 6 |
| 5 | 35 | 5 | 5 | 1 | 5 |
Anche in questo caso, all'aumentare del fattore lavoro la quantità prodotta aumenta. L'aumento del prodotto, però, avviene in misura via via decrescente: quindi ci troviamo di fronte ad una funzione di produzione a rendimenti decrescenti in quanto il prodotto marginale del lavoro è decrescente.
In questa ipotesi, all'aumentare del fattore lavoro diminuisce il prodotto marginale e, di conseguenza, diminuisce anche il prodotto medio. La diminuzione del prodotto medio è comunque inferiore rispetto alla diminuzione del prodotto marginale.
Attenzione!!!!: noi, nel nostro esempio, ci siamo fermati a 5 unità di lavoro e la quantità prodotta è sempre aumentata al crescere del numero degli operai impiegati. Se, però, l'azienda andasse avanti ad assumere dipendenti, si arriverebbe ad un punto in cui, essendo il prodotto marginale decrescente, la quantità totale prodotta non crescerebbe più, ma anzi inizierebbe a ridursi (si veda a tale proposito Legge dei rendimenti marginali decrescenti).
GRAFICO DELLA FUNZIONE DI PRODUZIONE A RENDIMENTI DECRESCENTI
Graficamente, la funzione riportata nell'esempio precedente, si presenta così:
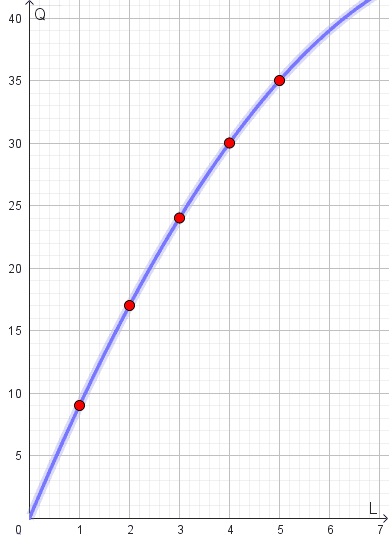
In questo caso la funzione è concava.