FORMA DEGLI ISOQUANTI

FORMA DEGLI ISOQUANTI

Abbiamo già visto uno dei possibili modi in cui può presentarsi graficamente un isoquanto. Abbiamo anche detto, però, che diverse possono essere le forme di tale curva.

A determinare l'aspetto dell'isoquanto è il tipo di tecnologia adottata per ottenere un dato prodotto e in modo più specifico la misura in cui i due fattori produttivi sono sostituibili tra loro.

La tecnologia adottata può essere:

• una tecnologia che non ammette sostituzioni tra i fattori produttivi;
• una tecnologia che ammette sostituzioni tra i fattori produttivi.

PERFETTI COMPLEMENTARI

Alcune tecnologie non permettono nessuna sostituzione tra i fattori produttivi: per ottenere un dato livello di produzione è possibile una sola combinazione tra il fattore lavoro e il fattore capitale.

In questo caso i fattori impiegati nel processo produttivo sono detti perfetti complementari.

Quando ciò si verifica la mappa di isoquanti si presenta ad angolo retto come riportato nell'immagine sottostante.

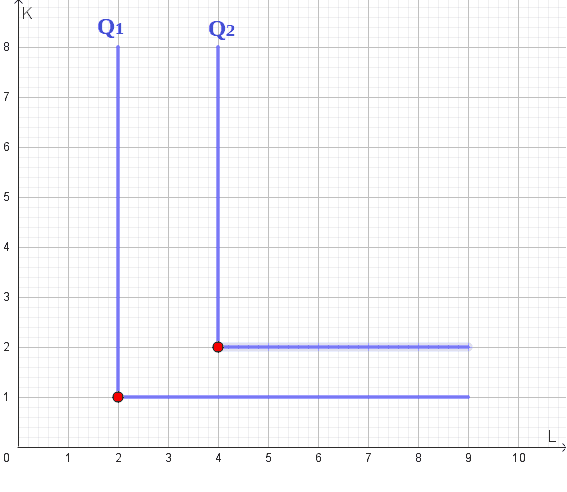
La quantità Q₁ può essere ottenuta in modo efficiente solamente combinando 2 unità del fattore lavoro e 1 unità del fattore capitale. Se noi andassimo ad aumentare la quantità di lavoro impiegata portandola, ad esempio, a 3 unità, fermo restando il capitale impiegato, la produzione sarebbe sempre pari a Q₁. La stessa cosa accadrebbe se andassimo ad aumentare la quantità di capitale utilizzato portandolo, ad esempio, a 2 unità, fermo restando il lavoro impiegato: anche in questo caso la produzione resterebbe fissa a Q₁.

Esempio: 5 programmatori hanno a disposizione 5 computer per svolgere la loro attività, in questo modo ognuno di loro utilizza un computer. Se venisse assunto un 6° lavoratore, uno di essi comunque non avrebbe modo di lavorare. Se, invece, i computer dovessero diventare 6, fermo restando il numero dei lavoratori a 5, un computer rimarrebbe inutilizzato. In entrambi i casi la produzione non cambierebbe.

Quando i fattori produttivi sono perfetti complementari si parla di produzione a proporzioni fisse dato che lavoro e capitale devono essere utilizzati in un rapporto costante.

La funzione di produzione, nel caso in cui l'isoquanto assume una forma ad angolo, è del tipo:

y = min (L, K)

TECNOLOGIE CHE AMMETTONO SOSTITUZIONI

La tecnologia ammette sostituzioni quando la stessa quantità di prodotto può essere ottenuta attraverso diverse combinazioni di fattori.

Quando la tecnologia ammette sostituzioni si possono avere due situazioni differenti:

• i fattori sono tra loro perfetti sostituti;
• oppure ci troviamo di fronte ad una tecnologia con saggio marginale di sostituzione tecnica decrescente.

PERFETTI SOSTITUTI

I fattori produttivi sono detti perfetti sostituti quando, per lasciare invariata la quantità prodotta, all'aumentare di una unità del fattore lavoro è necessario ridurre di una unità il fattore capitale.

L' isoquanto, in questo caso, è dato da una retta. Come sappiamo la pendenza di una retta è sempre costante (essendo rappresentata dal coefficiente angolare) e, in questo caso, è pari a -1: quindi, nell'ipotesi in cui i fattori sono perfetti sostituti il saggio marginale di sostituzione tecnica è costante è pari a -1 in qualunque punto dell'isoquanto.

La mappa di isoquanti si presenta così:

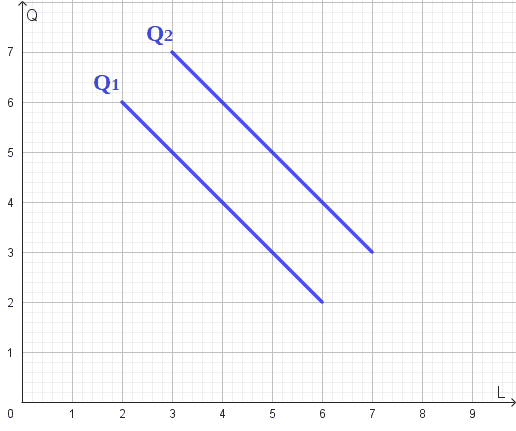
Esempio: ipotizziamo che l'impresa produca una quantità pari a Q₁ e, per ottenerla, impieghi 2 unità del fattore lavoro e 6 unità del fattore capitale. Se la quantità di lavoro utilizzata cresce di una unità (arrivando a 3 unità) la quantità di capitale impiegato deve ridursi di 1 unità (passando a 5 unità) affinché la quantità prodotta rimanga inalterata.

Può accadere che l'isoquanto sia rappresentato da una retta, ma con pendenza diversa da -1. Questa situazione si verifica quando i due fattori produttivi sono tra loro sostituibili in base ad un rapporto costante, ma non nella misura di una unità del fattore lavoro contro una unità del fattore capitale.

Anche in questo caso, quindi, il saggio marginale di sostituzione tecnica è:

• costante lungo tutto l'isoquanto;
• negativo perché, per lasciare la quantità prodotta inalterata, all'aumentare di un fattore deve diminuire l'altro;
• ma chiaramente sarà diverso da -1.

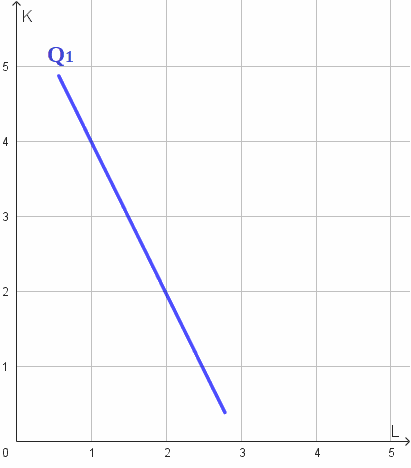
Esempio: nell'isoquanto disegnato sopra si nota che, per ottenere la quantità prodotta Q₁, utilizzando 1 unità del fattore lavoro occorre impiegare 4 unità del fattore capitale. Se il fattore lavoro viene aumentato a 2 unità, la quantità prodotta rimane invariata riducendo il capitale a 2 unità. Il SMST è, quindi, pari a -2.

La funzione di produzione, quando l'isoquando è una retta, è di tipo addittivo cioè assume il seguente aspetto:

y = aL + bK

TECNOLOGIE CON SAGGIO MARGINALE DI SOSTITUZIONE DECRESCENTE

Nella maggior parte dei casi i due fattori produttivi sono tra loro sostituibili entro certi limiti, ma la quantità del fattore capitale necessario per sostituire una unità del fattore lavoro diminuisce all’aumentare del lavoro impiegato: di conseguenza l’isoquanto risulterà essere convesso.

Il saggio marginale di sostituzione tecnica non è costante lungo l'isoquanto, ma decresce via via che viene ridotto l’impiego del fattore capitale ed aumentato l'impiego del fattore lavoro.

Il grafico si presenta nella forma che abbiamo già visto ampiamente nelle lezioni precedenti, ovvero:

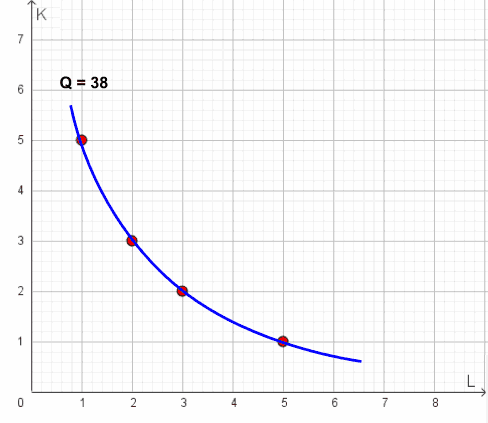
Un esempio di funzione di produzione il cui isoquanto è di tipo convesso è la funzione di Cobb-Douglas, ovvero:

y = A·L^α · K^β

con α, β > 0

GRADO DI SOSTITUIBILITA' DEI FATTORI PRODUTTIVI

Il grado di sostituibilità dei due fattori produttivi considerati determina la forma dell'isoquanto: l’isoquanto è tanto più convesso quanto meno sono sostituibili tra loro capitale e lavoro, e tanto meno convesso quanto più capitale e lavoro sono sostituibili tra loro.