GLI ISOQUANTI

FUNZIONE DI PRODUZIONE CON DUE FATTORI VARIABILI

Abbiamo già detto che, nel caso di una funzione di produzione a due input, si è soliti utilizzare gli isoquanti.

ISOQUANTI

Per isoquanto si intende una curva che esprime tutte le possibili combinazioni degli input capitale e lavoro che permettono di ottenere una determinata quantità di output.

Questa curva è chiamata anche isoquanto di produzione.

GRAFICO DI UN ISOQUANTO

Graficamente un isoquanto può presentarsi in modi diversi come avremo modo di vedere meglio in seguito.

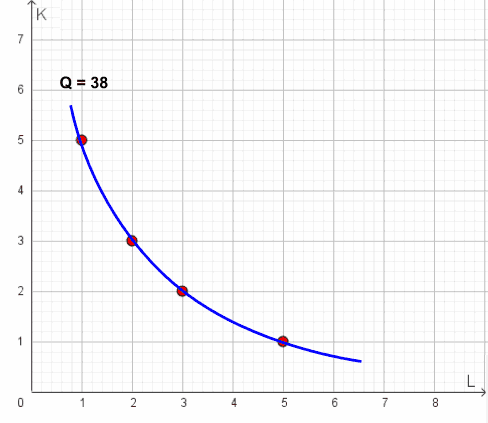
Ad ogni modo qui sotto abbiamo riportiamo un possibile isoquanto: questo è l'aspetto che più di frequente assume tale curva.

ESEMPIO

Per comprendere come si è giunti a questo grafico consideriamo un esempio: combinando tra loro il fattore lavoro e il fattore capitale in varie proporzioni si possono ottenere vari livelli di produzione. Essi sono riportati nella tabella sottostante.

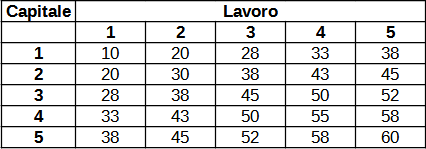
La tabella ci dice, ad esempio, che possiamo ottenere 38 unità di prodotto combinando tra loro:

• 1 unità del fattore lavoro e 5 unità del fattore capitale;
• oppure 2 unità del fattore lavoro e 3 unità del fattore capitale;
• o ancora 3 unità del fattore lavoro e 2 unità del fattore capitale;
• ed infine 5 unità del fattore lavoro e 1 unità del fattore capitale.

E' evidente che per ottenere la stessa quantità di prodotto, se riduciamo un fattore produttivo dobbiamo aumentare l'impiego dell'altro fattore.

L'isoquanto che abbiamo disegnato sopra rappresenta le diverse combinazioni possibili del fattore lavoro e del fattore capitale necessarie per ottenere 38 unità di prodotto.

CARATTERISTICHE DI UN ISOQUANTO

Da quanto abbiamo detto comprendiamo che, muovendoci lungo la curva di un isoquanto:

• la quantità prodotta rimane costante;
• a variare è il rapporto tra le quantità dei due input impiegati, cioè variano le proporzioni con le quali vengono impiegati K e L.