SAGGIO MARGINALE DI SOSTITUZIONE TECNICA E PRODUTTIVITA' MARGINALE DEI FATTORI PRODUTTIVI

RELAZIONE TRA SAGGIO MARGINALE DI SOSTITUZIONE TECNICA E PRODUTTIVITA' MARGINALE DEI FATTORI PRODUTTIVI

Cercheremo ora di capire quale relazione esiste tra il saggio marginale di sostituzione tecnica e la produttività marginale del fattore lavoro e del fattore capitale.

SMST

Abbiamo visto che la formula del saggio marginale di sostituzione tecnica è data da:

SMST = -ΔK/ΔL

PRODOTTO MARGINALE DEL FATTORE LAVORO E DEL FATTORE CAPITALE

Il prodotto marginale del fattore lavoro, tenuto costante il fattore capitale, è dato da:

MP_L = ΔQ/ΔL

mentre il prodotto marginale del fattore capitale, tenuto costante il fattore lavoro, è dato da:

MP_K = ΔQ/ΔK

SAGGIO MARGINALE DI SOSTITUZIONE TECNICA E RAPPORTO TRA LE PRODUTTIVITA' MARGINALI

Per capire la relazione tra queste formule partiamo dalla formula della produttività marginale del lavoro

MP_L = -ΔQ/ΔL

e da essa ricaviamo il valore della variazione della quantità moltiplicando entrambi i membri per ΔL:

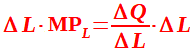
semplificando si ottiene:

ΔL · MP_L = ΔQ

Riscriviamo la formula in modo da mettere a primo membro la variazione della quantità prodotta:

ΔQ = ΔL · MP_L

Chiaramente, allo stesso modo, per quanto riguarda il capitale, possiamo scrivere che:

ΔQ = ΔK · MP_K

Se andiamo a variare sia il fattore lavoro che il fattore capitale, la variazione complessiva della quantità prodotta sarà data da:

ΔQ = ΔL · MP_L + ΔK · MP_K

Quando noi ci muoviamo lungo un isoquanto, la quantità prodotta rimane invariata, pur variando la quantità dei due fattori produttivi impiegati. Questo significa che, lungo un isoquanto, la variazione della quantità è pari a zero. In altre parole:

ΔQ = 0

Quindi, nella formula precedente, poniamo la variazione della produzione uguale a zero ed otteniamo:

0 = ΔL · MP_L + ΔK · MP_K

Volendo ricavare da essa il valore di ΔK possiamo scrivere:

-ΔK · MP_K = ΔL · MP_L

e dividendo ambo i membri per MP_k otteniamo:

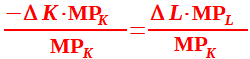
Semplifichiamo ed abbiamo:

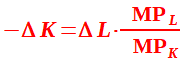
Ora dividiamo ambo i membri per ΔL:

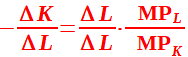
da cui otteniamo

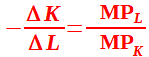
La formula scritta a primo membro non è altro che il saggio marginale di sostituzione tecnica. Quindi possiamo scrivere:

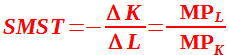
Pertanto possiamo dire che il saggio marginale di sostituzione tecnica è uguale al rapporto inverso tra le produttività marginali dei due fattori produttivi.

Attenzione!!!! Il saggio marginale di sostituzione tra due fattori è unguale al rapporto inverso dei due fattori. (Ovvero a numeratore della frazione presente a primo membro abbiamo la variazione del capitale, mentre la produttività marginale del capitale è presenta a denominatore della frazione del secondo membro. Così a denominatore della frazione presente a primo membro abbiamo la variazione del lavoro, mentre la produttività marginale del lavoro è presenta a numeratore della frazione del secondo membro. Notare anche che al primo membro abbiamo il segno negativo, mentre al secondo il segno è positivo).

PENDENZA NEGATIVA

Dalla relazione appena vista possiamo trarre la conclusione che, se i prodotti marginali del lavoro e del capitale sono positivi, il rapporto a secondo membro è positivo e, di conseguenza, il saggio marginale di sostituzione tecnica è negativo. Questo vuol dire che la pendenza dell'isoquanto è negativa.