RENDIMENTI DI SCALA E CURVE DI ISOQUANTO

RENDIMENTI DI SCALA E CURVE DI ISOQUANTO

In questa lezione ci occuperemo della relazione tra rendimenti di scala e curve di isoquanto: in altre parole andremo a vedere, attraverso degli esempi concreti, come si presentano le curve di isoquanto nel caso in cui i rendimenti di scala sono costanti, crescenti o decrescenti.

RENDIMENTI DI SCALA COSTANTI

Esempio: supponiamo che un'impresa, data una determinata tecnologia, sia in grado di ottenere 100 unità di prodotto utilizzando 2 unità di lavoro e 1 unità di capitale. Raddoppiando le quantità di lavoro e capitale impiegate, l'impresa riesce ad ottenere una produzione di 200 unità. Mentre triplicando le unità di lavoro e di capitale l'impresa ottiene 300 unità di prodotti.

Chiaramente ci troviamo di fronte a dei rendimenti di scala costanti.

La mappa di isquanti si presenta così:

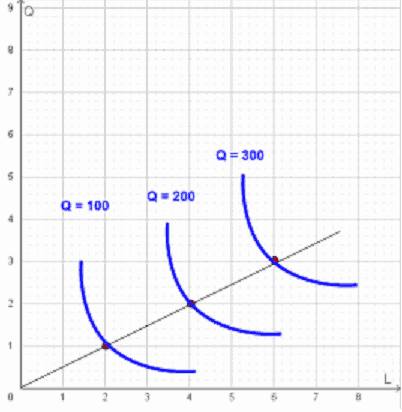
Notiamo che, nel caso di rendimenti di scala costanti, gli isoquanti sono equidistanti l'uno dall'altro all’aumentare della produzione.

RENDIMENTI DI SCALA CRESCENTI

Riprendiamo l'esempio visto in precedenza e supponiamo che raddoppiando le quantità di capitale e di lavoro impiegate, l'impresa riesca ad ottenere una produzione di 300 unità.

E' evidente che il rendimento di scala è crescente.

La mappa di isoquanti si presenterà nel modo seguente:

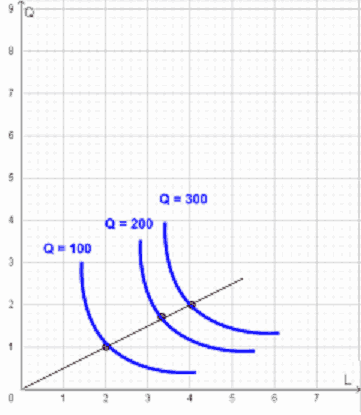
Si può notare dal grafico che, nel caso di rendimenti di scala crescenti, gli isoquanti si avvicinano all’aumentare della produzione.

RENDIMENTI DI SCALA DECRESCENTI

Riprendiamo ancora una volta il nostro esempio e supponiamo non è sufficiente raddoppiare le quantità impiegate di lavoro e capitale per ottenere una produzione di 200 unità

E' chiaro che ci troviamo di fronte ad un rendimento di scala decrescente.

La mappa di isoquanti si presenterà nel modo seguente:

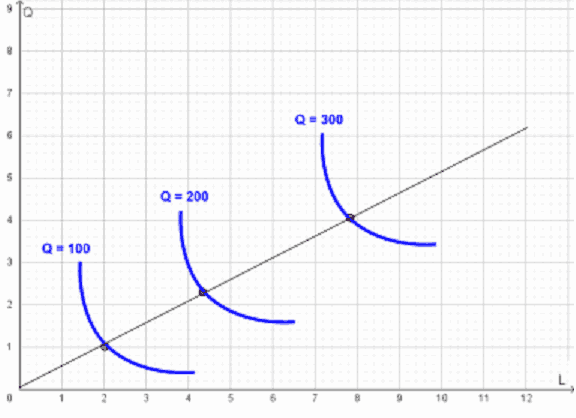
Nel caso di rendimenti di scala decrescenti, gli isoquanti si allontanano all’aumentare della produzione.