MAPPA DI INDIFFERENZA

DIVERSI LIVELLI DI UTILITA'

Nel parlare delle curve di indifferenza, fino a questo momento, le abbiamo considerate isolatamente: abbiamo, cioè, rappresentato sugli assi cartesiani una sola curva che rappresenta un certo livello di utilità.

Come sappiamo la curva mostra tutti i panieri che sono indifferenti per il consumatore perché egli trae da essi la medesima utilità, pari, nel grafico precedente ad U₁.

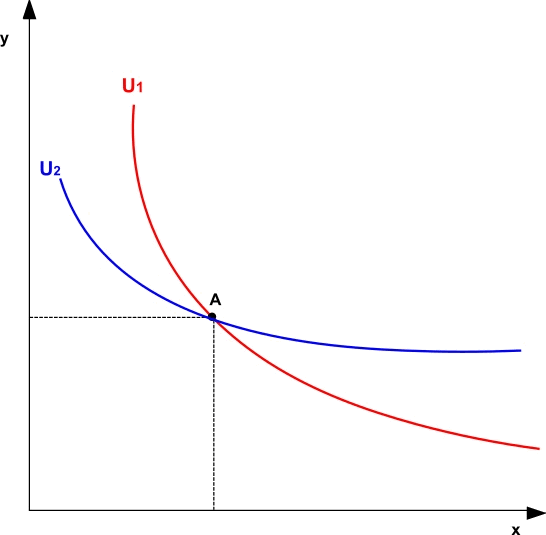
Consideriamo un punto A sulla curva di indifferenza U₁, formato dai beni x ed y nella misura x_a e y_a.

Riportiamo sul nostro grafico il punto B che individua un paniere formato dai beni x ed y nella misura misura x_b e y_b, tali che:

x_b > x_a
y_b > y_a

Il punto B si colloca in alto a destra rispetto al punto A e, come abbiamo già avuto modo di vedere, ad esso corrisponde un maggiore livello di utilità rispetto al punto A.

Chiamiamo l'utilità tratta dal punto B, U₂.

Individuiamo, ora, alcuni punti che rappresentano panieri dai quali il consumatore può trarre un'utilità pari a U₂ e colleghiamoli in modo da disegnare la curva di indifferenza U₂.

Possiamo andare avanti disegnando tutta una serie di curve di indifferenza.

MAPPE DI INDIFFERENZA

Quella che abbiamo appena disegnato prende il nome di mappa di indifferenza: essa non è altro che l'insieme delle curve di indifferenza che descrivono le preferenze di un dato consumatore rispetto ai beni x ed y.

Ad ogni curva di indifferenza corrisponde un diverso grado di soddisfazione: a curve più elevate corrispondono livelli maggiori di utilità e viceversa.

Date due curve di indifferenza, ad esempio U₁ e U₂, la seconda curva di indifferenza comprende panieri nei quali entrambi i beni sono contenuti in misura maggiore rispetto alla prima curva: per questo U₂ è situata, non solo più in alto rispetto ad U₁, ma anche più verso l'esterno nello spazio cartesiano.

La mappa di indifferenza rappresenta una descrizione completa delle preferenze del consumatore.

Ovviamente noi abbiamo disegnato solamente alcune curve che la compongono, ma nella mappa dovrebbero apparire curve di indifferenza estremamente fitte corrispondenti a livelli progressivi di soddisfazione.

LE CURVE DI INDIFFERENZA NON SI INTERSECANO

Due curve di indifferenza non si possono mai intersecare tra loro.

Vediamone il perché.

Proviamo a disegnare due curve di indifferenza alle quali corrispondono due diversi livelli di utilità U₁ e U₂ e, ipotizziamo che esse si intersechino:

Ora confrontiamo i punti B e C. Il punto B, situato sulla curva U₁, si trova più in alto e più a destra del punto C, che appartiene alla curva U₂: questo significa che l'utilità associata alla curva U₁ è maggiore rispetto all'utilità associata alla curva U₂. Ovvero:

U₁ > U₂

Ora confrontiamo i punti D ed E. Il punto D, situato sulla curva U₂, si trova più in alto e più a destra del punto E, che appartiene alla curva U₁: questo significa che l'utilità associata alla curva U₂ è maggiore rispetto all'utilità associata alla curva U₁. Ovvero:

U₂ > U₁

Chiaramente è impossibile che

U₁ > U₂ e contemporaneamente U₂ > U₁

Quindi è impossibile che le curve di indifferenza si intersechino.

LE CURVE DI INDIFFERENZA NON SONO SPESSE

Un'altra osservazione che possiamo fare è che le curve di indifferenza non sono spesse.

La spiegazione è molto semplice: disegniamo una curva di indifferenza piuttosto spessa.

Osserviamo che il punto A e il punto B si trovano sulla stessa curva di indifferenza. Quindi, teoricamente, da questi due panieri, il consumatore dovrebbe trarre la medesima utilità.

Ora però, guardando la posizione dei due punti, si nota che B è situato più a destra e più in alto rispetto ad A. Questo significa che l'utilità che il consumatore trae da B è maggiore rispetto all'utilità che il consumatore trae da A.

Si tratta di una contraddizione dato che i due punti si trovano sulla medesima curva di indifferenza: è per questo che le curve di indifferenza non possono essere spesse.