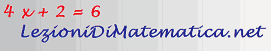ELASTICITÀ DELLA DOMANDA RISPETTO AL PREZZO NEL CASO DI DOMANDA LINEARE

DOMANDA LINEARE

Si parla di domanda lineare quando la curva della domanda è rappresentata da un linea retta.

Abbiamo già avuto modo di dire che l'elasticità della domanda varia al variare del punto considerato sulla curva anche quando la pendenza della curva è costante spiegandone il perché.

Ora vogliamo esaminare meglio come varia l'elasticità della domanda nel caso di domanda lineare.

FORMULA DELL'ELASTICITA' DELLA DOMANDA

Come abbiamo visto in precedenza, la formula per calcolare l'elasticità della domanda rispetto al prezzo è:

Quando la domanda è lineare la pendenza della curva è costante: quindi il primo fattore della nostra formula non varia qualunque sia il punto della curva preso in esame.

Invece, il rapporto tra prezzo e quantità varia lungo la curva.

Di conseguenza possiamo dire che il valore dell'elasticità varia da punto a punto lungo la curva della domanda.

ELASTICITA' DELLA DOMANDA E DOMANDA LINEARE

Quando la domanda è lineare la sua curva non è altro che l'equazione della retta che andiamo ad indicare nel modo che segue:

q = a - bp

dove:

q = quantità
p = prezzo
-b = coefficiente angolare = inclinazione della retta rispetto all'asse delle ascisse = Δq/ Δp

Di conseguenza, nel caso di domanda lineare, il valore dell'elasticità della domanda rispetto al prezzo può essere scritta come:

ε_dp = -b · (p/q)

Il simbolo ε si legge epsilon.

Chiaramente, volendone prendere il valore assoluto scriveremo:

|ε_dp| = |-b · (p/q)|

ELASTICITA' DELLA DOMANDA UGUALE A ZERO

Cominciamo a vedere cosa accade quando il prezzo è uguale a zero.

Innanzitutto osserviamo che, il prezzo è uguale a zero lungo l'asse delle ascisse.

Quando

p = 0

L'equazione della retta diventa:

q = a - bp

q = a - b · 0

q = a - 0

q = a

Quindi, quando p = 0 avremo che q = a.

Ora chiediamoci, in questo punto, qual è il valore della elasticità della domanda.

Poiché

ε_dp= -b · (p/q)

quando p = 0 avremo:

ε_dp= -b · (0/q)

ε_dp= -b · 0

ε_dp= 0

Quindi possiamo dire che l'elasticità della domanda rispetto al prezzo è uguale a zero quando il prezzo è uguale a zero, ovvero quando la curva della domanda incontra l'asse delle ascisse o potremmo dire, anche, sull'intercetta della domanda, ovvero nel punto a.

Chiameremo questo punto K.

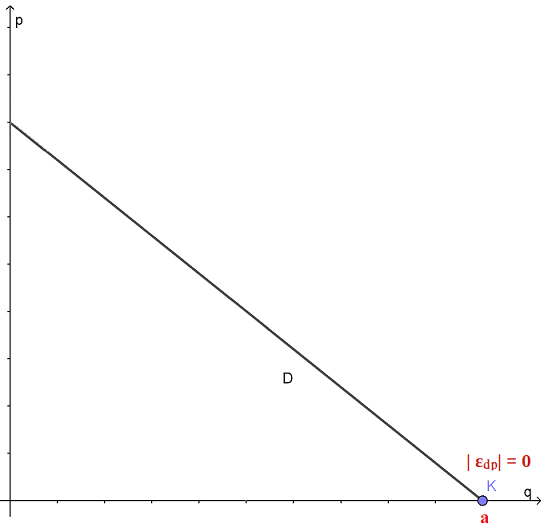
ELASTICITA' DELLA DOMANDA UGUALE AD INFINITO

Vediamo ora cosa accade quando la quantità è uguale a zero: ciò si verifica lungo l'asse delle ordinate.

Quando

q = 0

L'equazione della retta diventa:

q = a - bp

0 = a - bp

bp = a

p = a/b

Quindi, quando q = 0 avremo che p = a/b.

Ora chiediamoci, in questo punto, qual è il valore della elasticità della domanda.

Poiché

ε_dp= -b · (p/q)

Essendo q = 0 l'elasticità sarà pari a -∞.

Di conseguenza, ragionando sui valori assoluti, avremo che:

|ε_dp| = + ∞

Quindi possiamo affermare che, quando la quantità è uguale a zero, ovvero quando la curva della domanda incontra l'asse delle ordinate o potremmo dire anche sull'intercetta del prezzo, ovvero nel punto a, l'elasticità della domanda, in valore assoluto, è +∞.

Chiameremo questo punto W.

ELASTICITA' DELLA DOMANDA UGUALE AD UNO

Ora vogliamo capire quando l'elasticità della domanda, in valore assoluto, è uguale ad 1.

Partiamo da

ε_dp = - b · (p/q)

E poniamo

ε_dp = - 1

Avremo:

-1 = - b · (p/q)

Poiché l'equazione della retta è

q = a - bp

possiamo andare a sostituire, a denominatore della formula dell'elasticità, il valore di q ed avremo:

-1 = - b · (p/q)

Da cui ricaviamo il valore del p:

Ora andiamo a trovare quanto vale q nel momento in cui p vale a/2b. Per farlo andiamo a sostituire nell'equazione della retta, a p, il valore che abbiamo appena trovato. Avremo:

Quindi possiamo affermare che |ε| = 1 quando il prezzo è pari a a/(2b) e la quantità è pari a a/2: questo punto lo chiamiamo M.

PUNTO MEDIO DELLA FUNZIONE DI DOMANDA

Il punto M è esattamente il punto medio lunto il segmento WK. Infatti le coordinate del punto medio, che qui chiameremo M' vengono calcolate nel modo seguente:

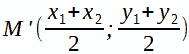
Sostituendo le coordinate dei punti W e K, avremo:

Quindi è evidente che

M = M'

ELASTICITA' DELLA DOMANDA NEGLI ALTRI PUNTI DELLA RETTA

Vediamo cosa accade negli altri punti della retta.

In tutti i punti al di sopra del punto medio M, escluso il punto W

∞ < |ε_dp| < 1

Quindi possiamo definire tale area come area elastica, poiché l'elasticità della domanda è maggiore di 1.

Mentre, in tutti i punti al di sotto del punto medio M, escluso il punto K

1 < |ε_dp| < 0

Questa area la chiameremo area anelastica, poiché l'elasticità della domanda è minore di 1.